Álgebra geométrica

En matemáticas , el álgebra geométrica incluye métodos geométricos , utilizados por los antiguos griegos , para establecer resultados ahora clasificados en la rama de las matemáticas llamada álgebra . Estas técnicas permiten la demostración de las propiedades elementales de la multiplicación , para realizar cálculos como la suma de los primeros números enteros, o números impares. Permiten establecer resultados como identidades notables o resolver una ecuación cuadrática . El álgebra geométrica también proporciona métodos de resolución más complejos, como los que muestran la existencia de números irracionales .

Si estos métodos son antiguos y corresponden a una visión de las matemáticas que ya no es la nuestra, todavía se utilizan en la enseñanza, ya sea para dar pruebas simples de ciertos resultados o para desarrollar una conciencia intuitiva de los resultados que la presentación algebraica lo haría más abstracto. .

El término "álgebra geométrica" ​​proviene de un libro del historiador de la ciencia Hieronymus Georg Zeuthen escrito en 1902 . Fue popularizado por Paul Tannery al año siguiente. Los Libros II y VI de los Elementos de Euclides en forma de corazón. Si una lectura contemporánea permite una interpretación algebraica de los resultados así demostrados, esta no era, sin embargo, la lectura de los griegos que no habían descubierto los principios fundamentales del álgebra. Por esta razón, esta lectura apócrifa de la ciencia griega es a veces criticada.

La expresión “álgebra geométrica” también se usa en matemáticas puras , por lo que corresponde a un concepto menos elemental. Designa una rama contemporánea de las matemáticas que consiste en asociar una geometría con una estructura de álgebra . Este aspecto se trata en el artículo Álgebra geométrica (estructura) . Los términos de geometría algebraica designan una rama diferente de las matemáticas, que consiste en el conocimiento adquirido esencialmente XIX XX y XX th  siglos y sigue la investigación matemática de noticias.

Propiedades de la multiplicación

Entero positivo

Podemos notar que 4 × 3 es igual a 3 × 4 y, de manera más general, “el producto de números enteros no depende del orden de los factores” .

Para estar convencidos de la precisión de este resultado, podemos considerar pequeños cuadrados, todos del mismo tamaño, ensamblados en filas de 3. Al unir verticalmente 4 filas de 3, obtenemos un rectángulo básico con 4 lados de cuadrados pequeños y altura 3 Este rectángulo, que se muestra en la figura de la izquierda, contiene 4 × 3 = 12 cuadrados pequeños. Aplicar un cuarto de vuelta al rectángulo no modifica el número de pequeños cuadrados que lo componen, lo que muestra que el resultado de 4 × 3 corresponde al número de pequeños cuadrados que componen el rectángulo asociado a la operación 3 × 4. Este resultado no depende no en valores 3 y 4, podemos elegir cualquier par de números enteros que podemos denotar una y b . La igualdad que se escribe a continuación traduce lo que se llama conmutatividad de la multiplicación:

a×B=B×a{\ Displaystyle a \ times b = b \ times a}.

La conmutatividad de la multiplicación no es la única propiedad ilustrada con la ayuda de la geometría. La figura de la derecha se puede leer de dos formas diferentes. Primero, el rectángulo grande es la suma de las áreas de los rectángulos azul y rojo. El razonamiento anterior muestra que su área es igual a 9 × 3 + 9 × 4. También podemos verlo como un solo rectángulo, si no tenemos en cuenta los colores, de área igual a 9 × (3 + 4). Por tanto, estas dos entradas corresponden al mismo número. Una vez más, el resultado es cierto no sólo para los números 9, 3 y 4, sino también para cualquier conjunto de tres números, que podemos escribir como un , b y c . Obtenemos el siguiente resultado, llamado distributividad de la multiplicación con respecto a la suma.

a×B+a×vs=a×(B+vs){\ Displaystyle a \ times b + a \ times c = a \ times (b + c)}.

Así, el uso de la geometría y más concretamente el cálculo de áreas permite establecer determinadas propiedades de multiplicación. Este principio es la base del álgebra geométrica.

Fracción

Para hacer geometría, los números enteros no siempre son suficientes. Una longitud puede ser la mitad de otra. Por lo tanto, los griegos se vieron obligados a establecer las reglas de funcionamiento que regían las fracciones. Una vez más, calcular áreas es útil. Para ilustrar este enfoque, intentemos sumar 1/6 y 4/9. Considere para eso un rectángulo cuya área es igual a 1. Elegimos dos cuadrículas que descomponen el rectángulo en pequeños rectángulos idénticos. Elegimos estas cuadrículas compatibles, es decir que la superposición de las cuadrículas sigue siendo una cuadrícula en pequeños rectángulos todos idénticos, como se ilustra en la siguiente figura:

La primera representación del rectángulo muestra que la fracción 1/6 está representada por una cuadrícula que corta el rectángulo en 6 pequeños rectángulos, la superposición de las cuadrículas crea 18 y 1/6 = 3/18. Finalmente obtenemos las igualdades:

16+49=318+818=1118{\ Displaystyle {\ frac {1} {6}} + {\ frac {4} {9}} = {\ frac {3} {18}} + {\ frac {8} {18}} = {\ frac {11} {18}}}.

En general, si una , b , c , y d son números enteros tales que ni b ni d son cero, entonces:

aB=D⋅aD⋅ByaB+vsD=a⋅D+vs⋅BB⋅D{\ Displaystyle {\ frac {a} {b}} = {\ frac {d \ cdot a} {d \ cdot b}} \ quad {\ text {et}} \ quad {\ frac {a} {b} } + {\ frac {c} {d}} = {\ frac {a \ cdot d + c \ cdot b} {b \ cdot d}}}.

El artículo detallado muestra cómo el proceso permite determinar todas las reglas de funcionamiento de las fracciones.

Aritmética geométrica

En los albores de las matemáticas griegas y hasta el matemático Pitágoras , se creía que todas las longitudes podían expresarse mediante lo que ahora se llaman fracciones , que Tannery expresa de la siguiente manera: "los pitagóricos parten de la idea, natural de cualquier hombre inculto, de que cualquier longitud es necesariamente conmensurable con la unidad. " . Estos matemáticos concluyeron que, para estudiar una figura geométrica, siempre se puede elegir una unidad de longitud tal que todos los segmentos representados en la figura tengan longitudes que se expresen como números enteros. La figura de la derecha ilustra esta situación. Representa dos segmentos de longitud 4/3 y 3/2, si la unidad elegida está indicada por la graduación azul. La unidad de la graduación roja es un sexto de la longitud de la azul, con la graduación roja, las longitudes son enteras e iguales a 8 y 9.

Esta observación y ciertas figuras geométricas permiten establecer resultados sobre números enteros, resultados que entran en la rama matemática llamada aritmética . Zeuthen considera que estas técnicas son aritméticas geométricas . Él cree que es una rama del álgebra geométrica porque los procedimientos son análogos.

Para hacer aritmética geométrica, las representaciones son de la misma naturaleza que la del párrafo Número entero , pero es posible simplificarlas. Los griegos habían notado que dibujar los rectángulos era innecesario. Las bolitas dentro de los cuadrados, que luego eran guijarros, fueron suficientes. El método consiste en representar un número mediante un conjunto de pellets según una figura geométrica. La asociación del número y la figura se llama número figurativo . El que se usó en el párrafo anterior para representar el 12 se llama número de rectángulo . Hay varias figuras catalogadas.

Suma de números primos

Al unir dos triángulos iguales como en la figura opuesta, obtenemos un rectángulo cuya longitud es una unidad mayor que su ancho (su área se llama número oblongo ). El artículo detallado muestra que deducimos la siguiente fórmula:

1+2+⋯+no=no×(no+1)2{\ Displaystyle 1 + 2 + \ cdots + n = {\ frac {n \ times (n + 1)} {2}}}.

Número cuadrado

Un número cuadrado es un número igual a cierto número entero multiplicado por sí mismo. Por ejemplo, 9 es un número cuadrado porque 3 × 3 = 9. Aparece en sentido figurado como un cuadrado. Para enumerar los primeros cuadrados, la aritmética geométrica puede ser útil. Supongamos, por ejemplo, que se conoce la lista hasta 7 × 7 = 49. Para encontrar el valor del siguiente cuadrado, con el lado 8, razonamos usando la figura de la izquierda. El número 8 × 8 se puede ver como la suma de 7 × 7 correspondiente a canicas rojas, 7 correspondiente a canicas verdes y 8 correspondiente a canicas azules. En general, tenemos igualdad:

(no+1)×(no+1)=no×no+no+(no+1){\ Displaystyle (n + 1) \ times (n + 1) = n \ times n + n + (n + 1)}.

Establecer la lista de los primeros números cuadrados es un ejercicio antiguo, ya realizado por los mesopotámicos. En ese momento, el conteo era base 60 . Hacer multiplicaciones como lo hacemos ahora habría supuesto aprender las tablas de multiplicar hasta el 60, un difícil ejercicio de memorización que no se impuso a los escolares mesopotámicos. Las mesas cuadradas, que existían entonces, fueron muy útiles. Por ejemplo, multiplicar 15 por 29 da:

15×29=15×(15+14)=15×15+14×14+14=225+196+14=435{\ Displaystyle 15 \ times 29 = 15 \ times (15 + 14) = 15 \ times 15 + 14 \ times 14 + 14 = 225 + 196 + 14 = 435}.

Los griegos heredaron el conocimiento mesopotámico y agregaron su propia interpretación que les permitió encontrar otros resultados. Habían notado que, si el lado de un número cuadrado es par, también lo es el número cuadrado, porque se descompone en la suma de dos números rectangulares iguales cuya base es igual al doble de la altura. La lógica geométrica nos permite entender que si el lado tiene una longitud impar, también lo es el área. La figura de la derecha lo ilustra en el ejemplo de 15 × 15. La representación del número cuadrado muestra que es la suma de un cuadrado, en rojo en la figura, que es par (está compuesto por tantas pastillas transparentes como oscuro), un número par (los puntos azules, que se dividen gráficamente en dos partes iguales) y un punto verde, aislado. Entonces, 15 × 15 es la suma de un número par (los puntos rojo y azul) y 1, que es un número impar.

Triplete pitagórico

Usando la cifra utilizada para calcular la lista de cuadrados, los griegos definieron un nuevo número figurativo, el número gnomon . Los puntos azules de la figura de la izquierda corresponden a un número gnomon: 9. Esta figura de la izquierda muestra que un cuadrado está formado por una secuencia de números gnomon, correspondiente a la secuencia de los primeros números impares. Lo que todavía se puede traducir por igualdad:

1+3+⋯+(2no-1)=no×no{\ Displaystyle 1 + 3 + \ cdots + (2n-1) = n \ times n}.

Este resultado permite construir triples pitagóricos si, como en la figura de la izquierda, el último gnomon es un cuadrado perfecto. La igualdad resultante de esta figura se escribe:

(1+3+5+7)+3×3=5×5{\ displaystyle (1 + 3 + 5 + 7) +3 \ times 3 = 5 \ times 5}.

Sin embargo, la suma de los números entre paréntesis corresponde a un número cuadrado; la igualdad todavía se escribe:

4×4+3×3=5×5{\ Displaystyle 4 \ times 4 + 3 \ times 3 = 5 \ times 5}.

Esta observación hace posible la construcción de series de tres números a , b y c , la verificación de un 2  +  b 2  =  c 2 , que llamamos el triplete de Pitágoras. Usando el teorema de Pitágoras , es posible construir triángulos rectángulos (con lados completos). Si, en lugar de elegir un ancho de 1 para el gnomon, le asignamos cualquier ancho, podemos encontrar un método que dé todos los triples pitagóricos. Se propone en el libro X de los Elementos de Euclides .

Suma de cubos

Los números de corte se construyen como cuadrados, excepto que esta vez el número representa el volumen y no la superficie. Los primeros cuatro números cúbicos son 1 = 1 3 , 8 = 2 3 , 27 = 3 3 y 64 = 4 3 . El siguiente razonamiento muestra que la suma de los primeros números cúbicos es siempre un número cuadrado.

En la figura opuesta, el lado del cuadrado más grande tiene por longitud el número triangular 1 + 2 + 3 + 4 = 10. Este cuadrado se descompone en una suma de gnomones cuyo ancho es 1, luego 2, luego 3, luego 4. Calcula el área del último. Esta zona naranja está compuesta por un cuadrado de lado 4 y dos rectángulos de ancho 4 y largo 1 + 2 + 3 = 6. El área del gnomon es por tanto igual a 2 × 4 × 6 + 4 2 = 3 × 4 2 + 4 2 = 4 3 .

Este razonamiento es cierto para todos los números gnomon de la figura: el razonamiento anterior muestra que el n -ésimo vale

2no(1+2+⋯+(no-1))+no2=2no(no-1)no2+no2=no3{\ Displaystyle 2n \ left (1 + 2 + \ cdots + (n-1) \ right) + n ^ {2} = 2n {\ frac {(n-1) n} {2}} + n ^ {2 } = n ^ {3}}.

Deducimos que la suma de los primeros n números cúbicos es el cuadrado del n- ésimo número triangular.

Ecuación cuadrática

Introducción por ejemplo

En la época de Pitágoras , es probable que los griegos supieran construir rigurosamente un pentágono regular. A priori, esta construcción parece referirse únicamente a la geometría, y así la concibieron los griegos. Una lectura moderna indica que esta pregunta está íntimamente ligada a la resolución de una pregunta algebraica, es decir, la resolución de un problema cuadrático .

La construcción de esta figura supone el conocimiento de las proporciones del triángulo isósceles formado por dos lados adyacentes del pentágono. Si elegimos la unidad igual a la longitud de un lado y si φ denota la base del triángulo, que corresponde a una diagonal del pentágono, la proporción se expresa de la siguiente manera:

(1)φ1=1φ-1o(2)φ2-φ-1=0{\ Displaystyle (1) \ quad {\ frac {\ varphi} {1}} = {\ frac {1} {\ varphi -1}} \ quad {\ text {o}} \ quad (2) \ quad \ varphi ^ {2} - \ varphi -1 = 0}.

Desde el punto de vista griego en la forma (1), la pregunta que se plantea es geométrica, es la de la determinación de una proporción, lo que Euclides llama de razón extrema y de razón media . Desde el punto de vista moderno y en la forma (2), la pregunta que se hace es algebraica, es la de la resolución de una ecuación cuadrática que tiene como única solución positiva el número dorado. Es posible que Hippasus de Metapontus , el probable autor de la construcción, usara un método importado de Babilonia, nuevamente basado en un gnomon.

La igualdad φ 2  = φ + 1 que resulta directamente de la igualdad (1) se lee de la siguiente manera: un cuadrado con lado φ tiene la misma área que un rectángulo con base φ + 1 y altura 1, resultado que se muestra en la figura de la izquierda. Restando del cuadrado y el rectángulo, el área de un gnomon de altura φ y ancho 1/2, notamos que un cuadrado de lado φ - 1/2 tiene un área igual a la suma de la de un cuadrado de lado 1 y el de un cuadrado de lado 1/2. Obtener la longitud φ se vuelve fácil con el teorema de Pitágoras , se basa en la figura de la derecha.

Demostración de igualdad (1)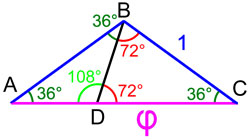

Sea ABC tres vértices consecutivos de un pentágono regular con lados de longitud 1. Un polígono convexo con n lados tiene, para el valor de la suma de sus ángulos, ( n  - 2) × 180 °, o para un pentágono de 540 °. Como el aquí estudiado es regular, el ángulo ABC tiene una medida de 540 ° / 5 = 108 °. Los otros dos ángulos BCA y CAB son iguales porque el triángulo es isósceles. Dado que la suma de las medidas de los ángulos de un triángulo es igual a 180 °, los otros dos ángulos tienen una medida de 36 °. Obtenemos el triángulo de la figura de la derecha.

Si trazamos la línea que pasa por B y dividimos el ángulo ABC de 108 ° en dos ángulos como en la figura de la derecha, uno de 36 ° y el otro de 72 °, dividimos el triángulo inicial en dos triángulos isósceles ABD y DBC. . Un análisis de ángulos muestra que el triángulo ABC es similar al triángulo ABD . Entonces es posible aplicar el teorema de Thales observando que AB  = 1, AC  =  AD  +  DC  = φ y BC  =  CD  = 1 porque el triángulo DBC es isósceles. Finalmente: AD  = φ - 1, y obtenemos:

AVSBVS=ABADyφ1=1φ-1{\ Displaystyle {\ frac {AC} {BC}} = {\ frac {AB} {AD}} \ quad {\ text {et}} \ quad {\ frac {\ varphi} {1}} = {\ frac {1} {\ varphi -1}}}.  

Identidad notable

Resolver una ecuación cuadrática, en el caso general, se resuelve usando tres identidades notables, expandiendo las expresiones ( a  +  b ) 2 , ( a  -  b ) 2 y ( a  +  b ) ( a  -  b ). Se demuestran usando las propiedades algebraicas de la suma y la multiplicación. Para los griegos, estos resultados son verdades geométricas, que se demuestran mediante un cuadrado, en azul en la figura de la derecha, y un gnomon, en verde y rojo.

Para establecer la siguiente fórmula, consideramos la figura de la derecha:

(1)(a+B)2=a2+2aB+B2{\ Displaystyle (1) \ quad (a + b) ^ {2} = a ^ {2} + 2ab + b ^ {2}}.

La longitud azul representa un y el rojo b . La expresión ( a  +  b ) 2 es igual al área del cuadrado grande de lado a  +  b . Es posible dividirlo en tres partes: la zona azul, correspondiente a un cuadrado de lado a y área a 2 ; la zona roja, que corresponde a un cuadrado de lado b y de área B 2, y la zona verde, que corresponde a dos rectángulos de longitud una y la anchura b . Cada rectángulo de la zona verde es de área igual ab , la zona verde es de área 2 ab . Encontramos la notable identidad (1).

La identidad se establece de la misma forma:

(2)(a-B)2=a2-2aB+B2{\ Displaystyle (2) \ quad (ab) ^ {2} = a ^ {2} -2ab + b ^ {2}}.

Esta vez, la longitud azul denota a  -  by la roja b . La expresión ( a  -  b ) ahora coincide con el área del cuadrado azul. El área del cuadrado azul puede verse como la diferencia entre el cuadrado grande, ahora lado a, y las dos áreas verdes y el área roja. El rectángulo formado por un área verde y el cuadrado rojo tiene un área ab . Si restamos de la zona del lado cuadrados a dos áreas de un rectángulo de longitud a y la anchura b , nos encontramos con el área del cuadrado azul resta del de la plaza roja, lo que da la siguiente identidad, desde del cual deducimos una igualdad equivalente a (2):

a2-2aB=(a-B)2-B2{\ Displaystyle a ^ {2} -2ab = (ab) ^ {2} -b ^ {2}}.

La identidad (3) se demuestra utilizando la misma figura:

(3)a2-B2=(a+B)(a-B){\ Displaystyle (3) \ quad a ^ {2} -b ^ {2} = (a + b) (ab)}.

Se utilizan las mismas convenciones que las que establecen la identidad (2). El área de la superficie a 2  -  b 2 corresponde al área del cuadrado grande restado del área del cuadrado rojo, es decir, el área del cuadrado azul sumada al área del dos rectángulos verdes. El rectángulo compuesto por la zona azul y una zona verde corresponde a un rectángulo de área a ( a  -  b ). Si movemos uno de los dos rectángulos verdes para colocarlo a lo largo del segundo rectángulo verde para formar un nuevo rectángulo, encontramos un rectángulo de longitud ( a  +  b ) ( a  -  b ). Este rectángulo tiene un área igual a la del cuadrado grande eliminado del área del cuadrado rojo, lo que demuestra la identidad (3).

Por lo tanto, todas las identidades notables utilizadas para resolver ecuaciones cuadráticas se interpretan y demuestran geométricamente. Como resultado, todas las ecuaciones cuadráticas se pueden resolver geométricamente. Esta lectura, que demuestra la equivalencia del contenido matemático de identidades notables con un conocimiento geométrico presente en el Libro II de los Elementos de Euclides, es obra de Zeuthen.

Resolver una ecuación cuadrática

Intentamos resolver la siguiente ecuación:

aX-X2=vscona2≥4vs{\ Displaystyle ax-x ^ {2} = c \ quad {\ text {con}} \ quad a ^ {2} \ geq 4c}.

El método se inspira directamente en cálculos similares a los utilizados para establecer identidades notables. Se ilustra en la figura siguiente.

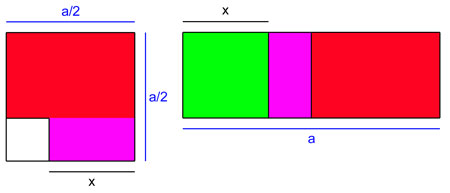
Primero, construimos un cuadrado con lado a / 2. por hipótesis, este cuadrado tiene un área mayor que c . Restamos del cuadrado, en la parte inferior izquierda un pequeño cuadrado de tal manera que la superficie roja y violeta sea de área exactamente igual ac .

En segundo lugar, notamos que la longitud x obtenida es también la altura del rectángulo rojo de la izquierda. Por lo tanto, es posible mover la zona violeta a la figura de la derecha y agregar a la izquierda de esta figura un cuadrado con el lado x . El área roja y violeta es, según la construcción de la figura de la izquierda, igual ac . Por construcción, la figura de la derecha tiene un área igual ac  +  x 2 . Esta zona es también igual a hacha , porque la figura es un rectángulo con la base de una y la altura x , que da la solución de la ecuación. Este método de resolución proviene directamente del Libro II de los Elementos de Euclides.

Irracionalidad

Los griegos finalmente se dieron cuenta de que su postulado inicial estaba equivocado. No todas las longitudes se expresan como una fracción de dos números enteros. Una pregunta, natural para un pitagórico, es la determinación de la fracción de números enteros que describen la proporción entre una diagonal y su lado, para un pentágono o un cuadrado. Esta razón no es una fracción de un número entero. Los métodos del álgebra geométrica son adecuados para abordar esta cuestión. En términos modernos, la pregunta es algebraica porque corresponde a la naturaleza de una solución de una ecuación cuadrática.

Los pitagóricos desarrollaron el culto al secreto sobre su conocimiento, por lo que es difícil saber con precisión cuándo, por quién y con qué métodos se realizaron el descubrimiento y luego la demostración. Se han imaginado varias hipótesis y, hasta la fecha, ninguna es unánime.

¿Un descubrimiento usando el pentágono?

El historiador Kurt von Fritz plantea la siguiente hipótesis: Hippasius, después de haber encontrado cómo construir el pentágono, habría buscado determinar la sección de razón extrema y media, es decir, la relación entre una diagonal y un lado de una regular. pentágono. Imagina que esta sección es una fracción n / m de dos números enteros. Un procedimiento para encontrar estos valores n y m consiste en construir un rectángulo con la base n y altura m . Intentamos llenar este rectángulo con cuadrados con el lado más grande posible. El primer valor del lado es my podemos colocar un solo cuadrado, en rojo sobre la figura.

Después de colocar el cuadrado rojo, el área restante es un cuadrado de lado m y n  -  m . Al multiplicar por n / m , notamos que el cuadrado es homotético con un cuadrado de altura my base n . Este resultado es consecuencia de la igualdad 1 / (φ - 1) = φ. Deducimos que luego podemos colocar un solo cuadrado, en azul oscuro en la figura y en el lado n  -  m . ¡Sobre todo, deducimos que el procedimiento nunca se detiene!

Este procedimiento, conocido desde los babilonios sobre el cálculo de la relación entre la diagonal y el lado de un cuadrado, permite dar una secuencia de fracciones que se aproxima cada vez mejor a la fracción φ. Obtenemos: 1, luego 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21 ..., es decir fracciones cada vez más cercanas a φ, con numeradores crecientes y denominadores. Este comportamiento no tiene sentido, los denominadores nunca deben exceder m . Los cuadrados rojos y luego azules necesariamente tienen lados completos. El historiador Maurice Caveing concluye que es razonable pensar que estas observaciones permitieron la realización de una asombrosa revelación  : el hecho de que todos los tamaños no son fracciones.

Posibles finales de la demostración

Hay otras formas de concluir a partir de la construcción anterior. Siempre asumimos que φ es un número racional, denotado n / m , y construimos un pentágono regular con lado my diagonal n . La figura de la derecha muestra cómo construir un nuevo pentágono, con lado n  -  my diagonal m , el lado y la diagonal del nuevo pentágono siguen siendo números enteros, pero esta vez más pequeños. Así podemos continuar indefinidamente. La serie de lados forma entonces una lista estrictamente decreciente e infinita de enteros positivos, lo cual es imposible. Tal razonamiento se llama en matemáticas un descenso infinito .

También hay una forma más rápida y sencilla de concluir. Con los mismos supuestos, elegimos, para el valor de n / m , una representación irreductible, es decir que m es el valor más pequeño que debe tomar el lado del pentágono para que el diámetro sea de longitud completa. El pentágono en rojo en la figura de la derecha muestra que es posible construir un pentágono con lado n  -  my diagonal completa. Esta contradicción nos permite concluir.

Existe un consenso relativamente amplio entre los historiadores de que Hippasus no pudo completar la demostración. Por ejemplo, para el descenso infinito, Caveing ​​comenta que: "Lo que falta en la prueba es sólo el axioma de Arquímedes , o un lema equivalente, que en el testimonio del propio Arquímedes no tenemos derecho a retroceder más alto". que Eudoxo de Cnidus  ” . Por lo tanto, Caveing ​​cree que durante el período hippasiano no fue posible ningún descubrimiento científico exitoso .

Raíz cuadrada de dos

La lógica presentada para el pentágono también se aplica a la diagonal del cuadrado. Encontramos rastros de ella en los libros de Euclides. La prueba por descendencia infinita se encuentra en el Libro X , en la Proposición 117. La prueba de que la fracción continua de un número racional es finita se encuentra en el Libro VII . Para este caso particular, este algoritmo ahora lleva el nombre de algoritmo euclidiano . También hay una demostración diferente, todavía presente en Euclides, y citada por Aristóteles " Demuestran que el diámetro del cuadrado es inconmensurable hacia el lado al mostrar que, si admitimos que es conmensurable con él, un número impar sería igual a un par. " El historiador Oskar Becker muestra que este razonamiento se basa en un conocimiento arcaico de los griegos en cuanto a la geometría aritmética, que pueden ser muy viejo. El método consiste en demostrar que "El doble de un número cuadrado nunca es un número cuadrado" .

Una reconstrucción de la posible demostración arcaica, basada en la aritmética geométrica, se basa en la figura de la izquierda. Todavía procede por lo absurdo. Consideramos que el número cuadrado más pequeño del lado es una suma de dos números cuadrados del lado b . El número cuadrado del lado a es par y, por lo tanto, a también lo es. El lado b es impar; de lo contrario, elegir una unidad dos veces más grande daría como resultado un nuevo valor dos veces más pequeño que a , cuyo cuadrado es la suma de dos cuadrados. Además, un cuadrado de lado b tiene la misma área que un rectángulo de altura una y dos veces tan grande como su base (en azul en la figura). Dicho rectángulo se compone de dos números cuadrados, por lo que es par y el cuadrado del lado b también lo es, así como b . El lado b es un número par y un número impar. Esta contradicción muestra que b no existe y pone fin a la prueba.

Una vez demostrada esta proposición, se obtiene la irracionalidad de la raíz cuadrada de dos aplicando el teorema de Pitágoras a la figura de la derecha. Si hubiera una unidad tal que todos los lados del triángulo rectángulo isósceles en la figura fueran números enteros, el resultado anterior sería falso.

Resultado

Una consecuencia de la existencia de irracionales es que las pruebas de propiedades establecidas sobre fracciones de números enteros al comienzo del artículo no abordan el caso general. Sin embargo, el uso de álgebra geométrica y un enfoque diferente todavía nos permiten demostrar que una fracción b / c es igual a ( ab ) / ( ac ) si una , b , c son tres positivos verdaderos números tales que una y c no son cero.

Para mostrar esto, se consideran dos líneas (negras en la figura de la derecha) que tienen intersección como un único punto A . Definimos los puntos B y C tal que la distancia AB es igual a b y AC a c . Los puntos B y C están cada uno en una de las líneas, como se muestra en la figura. El punto D (resp. E ) está ubicado en la línea AB (resp. AC ) y la distancia AD (resp. AE ) es igual a ab (resp. Ac ). El teorema de Tales indica que las líneas rojas son paralelas y que:

Bvs=a⋅Ba⋅vs{\ Displaystyle {\ frac {b} {c}} = {\ frac {a \ cdot b} {a \ cdot c}}}.

Podemos restablecer de esta manera todas las leyes que rigen las cuatro operaciones en cualquier número. Este trabajo se realiza en el Libro VI de los Elementos de Euclides , que por ello se considera álgebra geométrica.

Todas las demostraciones propuestas en este artículo utilizan el principio de medir una o más áreas. Esta regla es una característica del álgebra geométrica y esta prueba no es una excepción. La prueba de Euclides del teorema de Tales se basa en el mismo principio.

Si se utilizan siempre las demostraciones o ilustraciones anteriores, por su sencillez y su aspecto intuitivo, una construcción rigurosa de las reglas operativas en álgebra, como se lleva a cabo en el libro VI, no resulta sencilla ni intuitiva.

Historia de la ciencia

Dificultades

Los conceptos matemáticos griegos no son adecuados para un lenguaje algebraico. Esta observación es particularmente cierta para períodos tempranos, como el pitagórico. Un número es una colección de varias unidades ( uno no es un número), en nuestro caso corresponde a un entero positivo estrictamente mayor que uno. Una razón no es un número, sino una comparación de dos cantidades. La noción de razón adquiere un significado con la ayuda de la proporción. Cuatro cantidades un , b , c y d están en proporción si la relación de un : b es igual a la relación c : d . La unidad es una cantidad física elemental, como una longitud o un área que, asociada a números o razones, permite expresar las cantidades presentes en una figura geométrica. En la matemática helenística, no existe una verdadera multiplicación interna. La multiplicación de dos longitudes da el área de una figura plana, la multiplicación de dos números a y b corresponde más a la adición iterada un veces del número b que a un verdadero multiplicación. La diferencia entre sus conceptos y nuestro formalismo complica la comprensión de las matemáticas griegas. En consecuencia, la presentación de las ideas matemáticas contenidas en este artículo está, por razones de simplicidad de comprensión, muy lejos de un verdadero tratado de tiempo, como se encuentra en Euclides de Megara . Por ejemplo, el uso del símbolo 1 para determinar la sección de razón extrema y media no tendría sentido para un griego.

La segunda dificultad proviene de la escasez de fuentes antes de Platón . El V º y IV th  siglos BC. AD son casi vacíos en términos de tratados matemáticos. El conocimiento de los historiadores proviene de fuentes que se remontan a varios siglos y no siempre confiables, de estudios precisos sobre el significado exacto de ciertas palabras, que también se pueden encontrar en textos no matemáticos, análisis arqueológicos o incluso el estudio de importaciones de otras civilizaciones. Utilizando estas distintas indicaciones, los historiadores reconstruyen las posibles manifestaciones y las ubican en sus respectivas épocas y escuelas. Si, a lo largo del tiempo, todos los índices terminan dando una imagen coherente y consensuada a grandes rasgos, aún existen muchos puntos de divergencia, incluso en cuestiones importantes, entre los distintos especialistas.

Usos del término

En su libro de 1902, Zeuthen presenta el concepto de álgebra geométrica principalmente para describir el Libro II de Euclides y señalar que es equivalente a resolver una ecuación cuadrática. No toma precauciones oratorias particulares; atribuye a Euclides la voluntad de: "transportar, a las ecuaciones dadas numéricamente, la solución general encontrada para las ecuaciones cuadráticas" . Curtiduría está convencida de la veracidad de los testimonios, numerosos aunque a menudo tardíos y poco fiables, que atribuyen el descubrimiento de los irracionales a la época de Pitágoras. Piensa que este escándalo lógico real está en el origen del milagro matemático griego que son los Elementos de Euclides. Sin embargo, este descubrimiento solo puede tener lugar en la medida en que el dominio de las cuestiones secundarias sea suficiente. Estas preguntas, que caen dentro del dominio algebraico, el concepto de Zeuthen le pareció fructífero y lo adoptó al año siguiente. Para Curtiduría, lo que limitó a los griegos en el proceso no fue tanto la ausencia de un pensamiento algebraico como un vocabulario adaptado, que no poseían: “Lo que les falta a los matemáticos griegos son menos los métodos […] que las fórmulas específicas de la exposición de los métodos ” .

Si, como Heath , esta idea es adoptada a menudo por los historiadores de la época, suscita una primera polémica en la década de 1920. La forma de la matemática griega es geométrica, extraer una finalidad algebraica no es esencial. El gusto de todos y lo dice Jacob Klein. de esta manera: “Además, la mayoría de las historias clásicas intentan comprender las matemáticas griegas utilizando el simbolismo moderno, como si este último fuera extrínseco al contenido matemático, que podría revestirse de cualquier forma. " . Hablar de ecuaciones en Euclides, como hace Zeuthen, sugiere que los griegos ya tenían una incógnita sobre la que podían operar algebraicamente, como Al-Khawarizmi. Sin embargo, tal enfoque no existía antes de Diofanto.

Otto Neugebauer aporta, en la década de 1940, argumentos a favor de la tesis de Zeuthen y Tannery. Sus estudios de otras culturas matemáticas muestran que los griegos de la época de Pitágoras importaron técnicas mesopotámicas. Este conocimiento se basa en métodos y procedimientos de cálculo (pertenecientes a la misma familia que las fracciones continuas) que permiten aproximar raíces o incluso métodos de resolución de preguntas cuadráticas. Esta cultura es algebraica , en el sentido de que se basa en equivalentes de algoritmos (la palabra se inventará más adelante) cuyo objetivo es computacional. Como la construcción de la sección de razón extrema y media, muchas obras de la escuela de Pitágoras son traducciones de resultados mesopotámicos al lenguaje geométrico jónico. El concepto de álgebra geométrica se extiende a esta rama del conocimiento, ahora cubierta por el álgebra y que se demuestra en los griegos usando la medida de áreas. Allí encontramos la teoría de proporciones, presente en los libros V y VI que describen resultados ahora contenidos en los axiomas de un campo conmutativo , métodos para resolver y analizar la naturaleza de una solución de una cuestión de grado 2 presente en el libro II, o el aplicación del algoritmo de Euclides a proporciones, en el libro X, para demostrar su inconmensurabilidad. También contiene demostraciones, ya arcaicas en la época de Euclides, como la teoría de los pares y los impares.

Hasta la década de 1970, los historiadores ya no dudan en confiar en el concepto de Zeuthen y Tannery, incluso si algunos como Wilbur Knorr tomaron precauciones oratorias. Luego se relanza la controversia. Sabetai Unguru  (de) advierte la existencia de un diagrama ordinario, presente entre los chinos, los indios, los árabes o los europeos, que todos parten de la geometría para llegar, tras cierto grado de abstracción, a una formalización más algebraica. El patrón entre los griegos sería entonces al revés; a partir de una concepción de orientación algebraica, heredada de los mesopotámicos, se habrían movido hacia un sistema geométrico. Unguru no imagina este esquema realista. Esta posición, que cree que requeriría una profunda reescritura de la historia de las matemáticas griegas, es seguida por otros historiadores como Szabó.

La respuesta la dan varios especialistas, entre ellos van der Waerden, quien considera que Szabó concede demasiada importancia al formalismo, que la característica de los métodos pitagóricos aquí expuestos es su naturaleza computacional y algorítmica y que están bien heredados de los babilonios. Michael Sean Mahoney , que comparte la opinión de van der Waerden, comenta que los matemáticos fundadores del álgebra, como Al-Khawarizmi o Viète , se inspiran en gran medida en los textos de Euclides para construir sus teorías.

Pese a la polémica, muchos especialistas como Burkert, Itard o Caveing ​​hacen uso del concepto. Si los historiadores generalistas también lo utilizan para trabajos de divulgación, la expresión a menudo se adjunta a una advertencia como: "El término álgebra para una época en que la búsqueda de lo desconocido aún no es explícita, y menos aún el estudio de" ecuaciones ", debe ser utilizado con precaución " . El uso del término álgebra para las matemáticas antiguas no ha caído en desuso. Si el uso de la expresión álgebra geométrica a veces excede el contexto griego en la historia de la ciencia, el caso es lo suficientemente raro como para merecer ser señalado.

Herencia

Si la historia del álgebra geométrica comienza con Pitágoras, como indica Maurice Caveing: “hay razones para creer que la matemática griega no nació, como la hija de Métis, completamente armada con la cabeza de Zeus” . Para este autor, la escuela pitagórica hereda tanto la escuela jónica con las obras de Tales de Mileto como la herencia egipcia y mesopotámica . El trabajo de la escuela de Tales ya está modificando la orientación de las matemáticas griegas. Introduce la noción de prueba. Ciertamente no eran tan sofisticados como los encontrados en Euclides, sin embargo, esta especificidad griega ya está presente, diferenciándolos de sus predecesores. Una segunda especificidad de las matemáticas jónicas es su inclinación por la geometría. Los resultados dados a esta escuela son, por ejemplo, el hecho de que un triángulo isósceles tiene dos ángulos iguales o que un triángulo con una base del diámetro de un círculo y cuyo último vértice se ubica en el círculo es un rectángulo.

A diferencia de los jonios, la cultura mesopotámica es, al no ser calificada como algebraica, algorítmica. Las distintas tablillas que nos han llegado muestran las matemáticas en forma de problemas por resolver. El anotado BM 13901 , que contiene 24 preguntas cuadráticas , sugiere una ayuda geométrica para guiar el algoritmo utilizado. La tableta YBC 7289 muestra el conocimiento del resultado del algoritmo descrito en este artículo para el descubrimiento de la irracionalidad del tramo de razón extrema y media, pero esta vez aplicado a la diagonal de un cuadrado. Todos los ingredientes para descubrir la irracionalidad están presentes.

Escuela pitagórica

La escuela pitagórica cultiva el culto al secreto sobre su conocimiento. Por tanto, es difícil conocer con exactitud el contenido, fechar con precisión y asociar un nombre a los distintos avances. Sin embargo, es a esta escuela a la que debemos el nacimiento del álgebra geométrica griega. Esta escuela hereda el conocimiento babilónico, así como la orientación hacia la geometría y las demostraciones de los jonios. Esta fusión de conocimientos trajo un nuevo resultado: el álgebra geométrica que, en ese momento, todavía se limitaba en gran medida a la aritmética geométrica.

La ciencia mesopotámica aporta el poder del cálculo. Permite en geometría un progreso que probablemente nunca habían hecho los egipcios o los mesopotámicos. Un ejemplo lo dan las primeras demostraciones parciales del teorema de Pitágoras , que generalmente se atribuye a esta época. Solo se aplica en el caso de que los lados sean conmensurables, es decir, donde el triángulo corresponde a un triplete pitagórico, y utiliza una cuadrícula típica de la aritmética geométrica, ilustrada en la figura de la izquierda. En este ejemplo intentamos encontrar el área del cuadrado en varios azules, aparte de la hipotenusa de un triángulo rectángulo, cuyos otros lados son de longitudes 3 y 4. La agrupación de dos por dos de los triángulos interiores en el azul cuadrado permite concluir.

La potencia del enfoque les lleva a aplicarlo en casos de longitudes inconmensurables, sin necesariamente ser conscientes de una posible inconmensurabilidad. La construcción del pentágono impone la determinación del tramo de razón extrema y media, que corresponde a una cuestión de segundo grado. Los procedimientos computacionales mesopotámicos pueden superar esta dificultad. Esta construcción probablemente se llevó a cabo en la época de Pitágoras. Ilustra la orientación griega, el resultado no es una fracción que se aproxima al valor deseado, sino una construcción geométrica exacta.

El descubrimiento más importante que a menudo se atribuye a los pitagóricos y al álgebra geométrica es el de lo inconmensurable. Los elementos ya estaban casi presentes entre los babilonios, quienes sin embargo nunca hablaron de ello. Probablemente sea una actitud más especulativa y menos pragmática entre los griegos lo que marca la diferencia. Los mesopotámicos, sin embargo, también concibieron las matemáticas como una especulación, como muestra la tabla ilustrada en el párrafo anterior. Da la raíz de dos con una precisión de cinco lugares decimales, lo que no tiene ningún interés práctico dada su tecnología. Sin embargo, los mesopotámicos han elegido una numeración con notación posicional , un poco como nuestra notación decimal. Si esta notación es más práctica para las ciencias de la ingeniería, es menos adecuada que la escritura fraccionada de los griegos para el trabajo teórico sobre la irracionalidad. Un valor cuya notación posicional no termina, como 0.1111 ..., no significa irracionalidad.

De Pitágoras a Euclides

La escuela de Pitágoras proporciona un conocimiento aún lejos del que se encuentra, en álgebra geométrica, en los Elementos de Euclides. Para lograr este objetivo, las dificultades se pueden clasificar en tres categorías.

El primer conjunto de dificultades es lógico. El descubrimiento de los irracionales muestra la existencia de secuencias cuyo comportamiento no parece tener mucho sentido. El que se da como ejemplo en el artículo no es el más estudiado, los griegos prefieren el asociado a la diagonal del cuadrado. Se obtiene mediante un proceso más sencillo y tiene las mismas propiedades. Esta secuencia de proporciones parece difícilmente compatible con la hipótesis de que cualquier par de longitudes es conmensurable. Si se acerca cada vez más a la proporción deseada, nunca la alcanza. Muchos han visto en la Paradoja de Aquiles y la Tortuga un estudio lógico resultante de una reflexión sobre las secuencias resultantes del cálculo de los inconmensurables, es decir, una secuencia que se acerca infinitamente a su objetivo, sin tocarlo nunca. La ausencia de una base lógica suficiente habría llevado a Zenón de Elea a condenar el razonamiento pitagórico. Para resolver de manera confiable este escándalo lógico , para usar la expresión de Tannery, era necesario construir una lógica coherente. En la época de Aristóteles, el trabajo estaba hecho. Su análisis muestra claramente cómo articular el razonamiento a través del absurdo sin riesgo de error. Este autor utiliza varias veces el ejemplo del hecho de que la diagonal de un cuadrado no es conmensurable con su lado.

El segundo conjunto de dificultades se refiere a la modificación del marco conceptual impuesto por lo inconmensurable. En la época de Pitágoras, el teorema que lleva su nombre es la igualdad entre números —siempre enteros con los griegos—; con Euclides, este teorema es una igualdad entre áreas, que esta vez no tienen ninguna razón para poder ser representadas por números. Esta modificación impone una reconstrucción total de las matemáticas, hay que revisar también la demostración del teorema de Tales y todas las demostraciones que ahora deben dejar su matriz conmensurable y ya no pueden basarse en una lógica basada en la aritmética geométrica. Dominar los inconmensurables supone también una aritmética más fuerte, para llevar a cabo el razonamiento presentado para el descubrimiento de los irracionales. En Euclides, el razonamiento que muestra que en el caso de cantidades conmensurables el algoritmo se detiene, se ha vuelto riguroso. Sin embargo, ha dejado su origen de aritmética geométrica, este algoritmo ya no proporciona la unidad de la figura (es decir, la unidad más grande que permite expresar las dos longitudes como múltiplos de la unidad) sino el máximo común divisor entre dos. números. El historiador Jean Itard se expresa así sobre la teoría de los números en Euclides: "Está casi completamente libre de aritmo-geometría, numeración práctica y logística, pero permanece estrechamente vinculada a la teoría. Informes" .

Finalmente, la tercera serie de dificultades consiste en desarrollar las herramientas que permitan comprender el comportamiento asintótico de la extraña secuencia de los orígenes del descubrimiento. De una forma u otra, impone un cierto dominio del fenómeno límite , que luego es tratado por el agotamiento . El Libro V de los Elementos permite construir un universo admitiendo los inconmensurables y los fenómenos de convergencia, conservando las propiedades algebraicas ahora expresadas en forma de axiomas como la distributividad de la multiplicación frente a la suma en el cuerpo de los reales. . Esta obra no deja de tener consecuencias, impone lo que se convertirá en el axioma de Arquímedes y permitirá fundamentar sólidamente el argumento del descenso infinito.

Álgebra geométrica en Euclides

Dos siglos separan a Pitágoras de Euclides. De alguna manera, el propósito no ha cambiado. Todavía encontramos en el libro los métodos que prueban las propiedades algebraicas de las proporciones, como la distributividad presente en los libros V y VI, los procedimientos para la resolución de preguntas cuadráticas y el uso de la anféresis - equivalente a una fracción continua . inconmensurabilidad de ciertas proporciones. En otros aspectos, la teoría se metamorfosea. Se basa en una lógica axiomatizada, la teoría de las proporciones tiene en cuenta los inconmensurables y la aritmética utilizada ya no tiene mucho que ver con la de Pitágoras. En consecuencia, todas las vías de demostración presentadas en este artículo se han explorado con rigor con éxito y las paradojas ya no existen. Si la aritmética geométrica de Pitágoras descubre lo inconmensurable, el álgebra geométrica de Euclides los domina. El gran ausente sigue siendo el número que todavía se limita a números enteros. Eudoxo no puede definir el axioma de Arquímedes como lo imaginamos hoy. Este axioma depende de la cantidad considerada y el matemático en última instancia solo se ocupa del caso de áreas

Si los fundamentos introducidos en la época de Pitágoras permanecen imbuidos del origen mesopotámico, el propósito se modifica. Un algoritmo como la antiféresis ya no se usa para aproximar una proporción, sino para establecer la propiedad de inconmensurabilidad. Es notorio el desprecio por los cálculos de los griegos, Heródoto se detiene con una división por 48. Para Szabó, esta modificación de la finalidad no es la más importante. No existe un formalismo algebraico entre los griegos y el hecho de que el objeto principal de estudio sea una proporción y no un número no es un factor favorable. Esta ausencia de formalismo algebraico es la prueba de una orientación geométrica, lejos de las preocupaciones e ideas de un precursor del álgebra como Diofanto. Con Euclides, la idea de una ecuación no aparece ni puede aparecer. Operar en un desconocido y ya no solo en números, es casi imposible aquí. Sin embargo, la ecuación y lo desconocido a menudo se consideran el certificado de nacimiento del álgebra.

Para van der Waerden, la característica del álgebra es la demostración y el uso de una estructura. El trabajo de Eudoxo consiste en asegurar la existencia de un mundo con propiedades algebraicas, como la distributividad o la conmutatividad de una multiplicación de proporciones, respetando una relación de orden. Cette question est fondamentalement algébrique et le fait qu'Eudoxe trouve un résultat équivalent aux coupures de Dedekind n'est pas le fruit du hasard, ils cherchent tous deux à résoudre la même question, indépendamment du vêtement ou du formalisme choisi et la matière mathématique reste la misma. Asimismo, el Libro II establece propiedades comúnmente denominadas identidades notables. Son válidos en todos los anillos conmutativos y por tanto en el de las proporciones geométricas de los griegos El hecho de trabajar en una estructura con vocación geométrica no modifica en modo alguno su naturaleza algebraica. El uso entre los griegos de la antiféresis apunta a una clasificación de los inconmensurables. Esta idea, que se impulsará mucho más en la teoría de Galois , es también una cuestión algebraica. En conclusión y para van der Waerden, si la finalidad y el formalismo son geométricos, la naturaleza misma del álgebra geométrica permanece sin cambios desde Mesopotamia.

Para los fundadores del álgebra árabe y europea, el álgebra geométrica es esencial. La lógica de resolver una ecuación de Al-Khawarizmi solo es posible en la medida en que se establecen las propiedades algebraicas del conjunto del que se derivan los coeficientes del polinomio . En su tratado Abrégé du calcul par la restauration et la compare, Al-Khawarizmi se basa en Euclides para establecer la relevancia del enfoque, al igual que su discípulo Abu Kamil . El libro V es el único que propone una construcción algebraica suficientemente sólida para representar la estructura de números reales positivos. Euclides, al no tener una forma de expresar lo inconmensurable, desarrolla en un lenguaje geométrico un equivalente de identidades notables, en el sentido de van der Waerden, de manera genérica. Esta genéricaidad es fundamental para los primeros algebristas árabes que no tienen parámetros y deben contentarse con ilustrar sus principios con ejemplos. En el XVI °  siglo en Europa, Vieta llena este vacío y se desarrolla el concepto de parámetro, la generalización de álgebra y permitiendo la expresión de los resultados más potentes, tales como fórmulas de Vieta . Para Viète, la construcción del álgebra geométrica sigue siendo esencial. Así, durante casi 2000 años, el álgebra geométrica fue una herramienta esencial para los algebristas europeos y árabes. Este elemento convence a Mahoney del carácter algebraico de la teoría.

Apéndices

Bibliografía

• Hieronymus Georg Zeuthen , Historia de las matemáticas en la antigüedad y la Edad Media , Gauthier-Villars ,1902( leer en línea )Zeuthen lanza el concepto de álgebra geométrica en esta referencia. Con respecto a una concepción contemporánea de la historia de la ciencia, está fechada. Por ejemplo, presta a los griegos la capacidad de resolver ecuaciones, algo que los especialistas de nuestro tiempo ya no hacen.
• Paul Tannery , Nociones de matemáticas , París, Delagrave,1903( leer en línea )Tannery realmente lanza el concepto dándole un papel y un significado histórico.
• (en) Thomas Heath, Los trece libros de los elementos de Euclides, Libros 1 y 2 , Cambridge, 1926La edición de los libros de Euclides comentada por Heath es una de las referencias sobre el tema.
• (en) Otto Neugebauer , Las ciencias exactas en la antigüedad , Dover ,1969, 240  p. ( ISBN  978-0-486-22332-2 )Esta referencia estudia la influencia de los mesopotámicos sobre los griegos.
• (en) Walter Burkert , Lore y ciencia en el pitagorismo antiguo , Harvard University Press ,1972, 535  p. ( ISBN  978-0-674-53918-1 , presentación en línea )Este libro es la principal referencia utilizada en el artículo para el período pitagórico.
• Euclide ( traducción de  Bernard Vitrac), The Elements [ detalle de las ediciones ](1990-2001) ( ISBN  978-2130432401 )Este libro es una de las ediciones francesas de referencia sobre Euclide. En las páginas 366-376 encontramos una descripción de la controversia que rodea al concepto de álgebra geométrica.
• Maurice Caveing , La figura y el número: investigación sobre las primeras matemáticas de los griegos , Éditions du Septentrion , 1998a, 424  p. ( ISBN  978-2-85939-494-3 , presentación en línea )Este tratado sobre la historia de las matemáticas griegas del período helenístico se refiere con frecuencia al concepto del artículo.
• Maurice Caveing , Irracionalidad en las matemáticas griegas hasta Euclides , Éditions du Septentrion, 1998b, 343  p. ( ISBN  978-2-85939-539-1 )
• Árpád Szabó , El amanecer de las matemáticas griegas , Vrin,2000, 367  p. ( ISBN  978-2-7116-1279-6 , presentación en línea )Árpád Szabó es uno de los manifestantes del concepto. Explica las razones de su opinión en un apéndice de este libro.
• (en) Bartel L.van der Waerden, Geometry and Algebra in Ancient Civilizations (1983, reed. Springer 2002) reedición ( ISBN  978-3540121596 )Van der Waerden es un famoso historiador de las matemáticas antiguas, pero también un algebrista que resolvió el decimoquinto problema de Hilbert .

Notas

1. Una lectura real de textos matemáticos antes de Euclides no es tan simple. Para los griegos, los números son siempre enteros. Su equivalente de nuestros números racionales corresponde a lo que ellos llaman un logo, que no es un número sino una proporción.
2. Ver el artículo Ecuación de segundo grado .
3. Ver el artículo Continuous Fraction .
4. historiadores no han determinado si el descubrimiento provino de un análisis de la diagonal del cuadrado o la del pentágono. Menos aún han determinado el razonamiento detrás de este descubrimiento. Caveing ​​sospecha que el primer descubrimiento tuvo lugar en la secuela asociada con el razonamiento presentado en este párrafo.
5. El descenso infinito se presenta en el artículo detallado, la demostración del carácter finito de una fracción continua de un número racional se demuestra en el artículo Fracción continua .
6. Una pieza escrita en -480 por Epicharme parece referirse al conocimiento del principio de pares e impares.
7. Una demostración, basada en aritmética geométrica, se da en la sección de números cuadrados .
8. La demostración de Euclides se da en el artículo detallado.
9. Es a menudo al propio Pitágoras a quien los testimonios atribuyen el descubrimiento de lo irracional.
10. Para esta pregunta, consulte el artículo Teoría de ecuaciones .
11. Lo cual sigue siendo un anacronismo porque este término proviene de Al-Khawarizmi, un persa que no aparece hasta más de mil años después
12. Si esta idea de atribución a los pitagóricos es compartida por Tannery, Zeuthen, Heath, Becker, Fritz, Szabó, Michel  (it) o Caveing, otros como Neugebauer imaginan un descubrimiento posterior y otros, como Burkert, no hablan .
13. No fue hasta el XIX °  siglo que los defectos en la construcción de la lógica serán resaltados.
14. Estrictamente hablando, sería necesario sumar las proporciones negativas para obtener una estructura de anillo, lo que los griegos no hicieron.

Referencias

Referencias didácticas:

1. Charles-E. Jean, "  número figurativo  ", en Récréomath .
2. Esta presentación está inspirada en: Claudie Asselin-Missenard y André Deledicq , “Los cuadrados del 1 al 25”, Pruebas matemáticas y juego de preguntas , Les éditions du Kangourou, 2010, p.  22 .
3. Esta presentación está inspirada en: Claudie Asselin-Missenard y André Deledicq , “Les squares de Babylone”, Pruebas matemáticas y juego de preguntas , Les éditions du Kangourou, 2010, p.  24 .
4. Gérard Villemin, “  Deterioros, Carrés et Cubes  ”, sobre Números - Curiosidades, teoría y usos .

Referencias académicas:

1. Esta cita está tomada del primer ejemplo del uso de la aritmética geométrica por Zeuthen 1902 , p.  31.
2. “Entre las diversas lagunas intentó, y con éxito, por los matemáticos griegos [...] es la parte de” álgebra geométrica “(expresión de Zeuthen) que es la aplicación de las áreas. » Paul-Henri Michel y Jean Itard , Ciencia antigua y medieval, desde los orígenes hasta 1450 , Quadrige,1994, p.  231-233 .
3. Paul Tannery Scientific memorias , París-Toulouse, Privat, 1912, I, p.  268 .
4. Más precisamente, Zeuthen considera que la aritmética geométrica es una introducción al álgebra geométrica  : Zeuthen 1902 , p.  31.
5. Zeuthen no es el único historiador de la ciencia que considera que la aritmética geométrica es una rama del álgebra geométrica: Árpád Szabó  (de) usa este término para describir los resultados aritméticos conocidos por los babilonios y demostrados geométricamente por los griegos, cf. (en) Árpád Szabó , The Beginnings of Greek Mathematics , Springer,1978, 358  p. ( ISBN  978-90-277-0819-9 , presentación en línea ) , p.  31 (traducido de (de) Anfänge der griechischen Mathematik , de Gruyter,1969( leer en línea ) ; Versión francesa: Los inicios de las matemáticas griegas , J. Vrin,1977, 403  p. ( ISBN  978-2-7116-0691-7 ) ; no confundir con Szabó 2000 ).
6. Otros historiadores utilizan el término aritmo-geometría para designar esta técnica matemática: Jean Itard, Les livres arithmétiques d'Euclide , Hermann, 1961, p.  77 .
7. Burkert 1972 , p.  428. cuestionable
8. Este es el primer ejemplo de aritmética geométrica de Zeuthen 1902 , p.  33.
9. Para más detalles, ver: Christine Proust , "  Le calcul sexagesimal en Mésopotamie  ", p.  20 .
10. De manera más general, los pitagóricos de -480 probablemente conocían la “teoría de los pares e impares” y sabían cómo deducir la paridad de un producto, conociendo la paridad de los factores: (de) O. Becker , “  Die Lehre von Geraden und Ungeraden im neunten Buch der euklidischen Elemente  ” , Quellen und Studien sur Geschichte der Mathematik, Astronomie und Physik , b, vol.  3,1936, p.  533-553 .
11. Este método se describe en Caveing ​​1998b , p.  91.
12. Zeuthen 1902 , p.  31.
13. (en) Thomas Little Heath , A History of Mathematics griega , vol.  1: De Thales a Euclid , CUP ,2013( 1 st  ed. 1921), 468  p. ( ISBN  978-1-108-06306-7 , presentación en línea ) , p.  160.
14. Desde el principio, estas preguntas cuadráticas han estado en el corazón del álgebra geométrica: Zeuthen 1902 , p.  42-43.
15. Jean-Luc Périllié , Symmetria et racionalité harmonique: origen pitagórico de la noción griega de simetría , L'Harmattan ,2005, 282  p. ( ISBN  978-2-7475-8787-7 ) , pág.  144.
16. DahanPeiffer , pág.  74.
17. Zeuthen 1902 , p.  36-44.
18. Es equivalente al de Zeuthen 1902 , p.  39.
19. Ver explicaciones en DahanPeiffer , p.  60.
20. Esta asociación entre álgebra geométrica y el estudio de la irracionalidad es frecuente. Walter Burkert indica "  La conquista de lo irracional en la matemática griega, y con ello el desarrollo del" álgebra geométrica "...  "  : Burkert 1972 , p.  465.
21. Walter Burkert , especialista en Pitágoras y su escuela, especifica: "  La única certeza sobre el descubrimiento de la irracionalidad es que Teodoro de Cirene demostró que √n (para n = 3, ... 17 y no un cuadrado perfecto) es irracional .  ” En Burkert 1972 , p.  439 cuestionable .
22. El objeto de Caveing ​​1998b es revisar estas diferentes hipótesis.
23. (en) Kurt von Fritz, "El descubrimiento de la inconmensurabilidad por Hippasus de Metapontum", Ann. de Matemáticas. (2) , vol. 46, n ° 2, 1945, pág.  242-264 DOI : 10.2307 / 1969021 .
24. El método se describe en Caveing ​​1998b , p.  99-119.
25. Este algoritmo se describe en el artículo: Benoît Rittaud, “¡  Para un matemático desconocido!  », Sobre Bibnum .
26. Caveing 1998b , p.  117.
27. Maurice Caveing, “  Sobre el comienzo de las matemáticas griegas. Reflexiones sobre la obra de A. Szabo  ”, Revue d'histoire des sciences , vol 32, 1979, p.  168 .
28. Aristóteles, Analíticos I, 23.
29. Becker, 1934 .
30. La siguiente referencia contiene la cita: "Designamos bajo el nombre de álgebra geométrica griega, toda una serie de problemas que aparecen en el libro dos y en el libro seis de los Elementos de Euclides, que se expresan y resuelven geométricamente [...]"  : Eliane Cousquer, "  De la teoría de las proporciones a la teoría de los números reales  ", Laboratorio LAMIA , 1995, p.  8 .
31. (en) Wilbur Richard Knorr , La evolución de los elementos euclidianos: un estudio de la teoría de magnitudes inconmensurables y su importancia para la geometría griega temprana , Springer,1974, 374  p. ( ISBN  978-90-277-0509-9 ) , pág.  15.
32. Aristóteles , Metafísica , 1052b, p.  20-28 .
33. "Señalemos, sin embargo, que la teoría griega de las relaciones presenta un punto débil, a saber, que su conjunto está provisto sólo de una estructura de grupo y no de una estructura corporal. Este grupo, es cierto, se completa con algunas aplicaciones del todo sobre sí mismo, "inversión", "composición", "separación", que son, en el fondo, las transformaciones básicas de nuestro grupo modular. » Michel e Itard 1994 , p.  231-233.
34. Ver sobre este tema el párrafo titulado Sobre la interpretación de las fuentes  : Knorr 1974 , p.  5.
35. Toda la parte I de esta referencia es una glosa sobre el significado exacto de la palabra griega dynamis , que permite atribuir un papel a los eleatans  : Szabó 1978 , p.  31.
36. Aquí, el autor retoma un antiguo análisis de Heath para evaluar el conocimiento de Hippasius sobre el pentágono: Périllié 2005 , p.  147.
37. Esto es lo que el autor hace en gran medida en su primer capítulo The Breakthrough of the Ionians  : Caveing ​​1998a , p.  31-75.
38. Zeuthen 1902 , p.  43.
39. Paul Tannery, Para la historia de la ciencia helénica , BiblioBazaar, reed. 2008 ( ISBN  978-0559304156 ) , pág.  251 .
40. Curtiembre 1903 , cap. II, párrafo 189.
41. Cita de recuperación (por) Michael S. Mahoney , "  Otra mirada al análisis geométrico griego  " , Arch. Hist. Exact Sci. , vol.  5,1968, p.  18-348.
42. Heath , 2013 , p.  153.
43. Bernard Vitrac, ¿Podemos hablar de álgebra en las matemáticas griegas antiguas? CNRS, UMR 8567, Centro Louis Gernet, pág.  3 .
44. Traducción libre de la cita: “  Por otra parte, la mayoría de las historias convencionales intentan comprender las matemáticas griegas sí con la ayuda del simbolismo moderno, como si éste fuera un conjunto externo de forma que puede ser adaptado a cualquier deseables contenidos .  " Jacob Klein, Pensamiento matemático griego y el origen del álgebra , Publicaciones de Dover (traducción de un libro de 1934 en 1992) ( ISBN  978-0486272894 ) , p.  5 .
45. Luis Radford , "  Diofanto y álgebra presimbólica  ", Boletín AMQ ,1991( leer en línea ).
46. Neugebauer 1969 , p.  145-176.
47. Michel y Itard 1994 , p.  231-233.
48. Knorr 1974 , p.  11.
49. (en) S. Unguru, "Sobre la necesidad de reescribir la historia de las matemáticas griegas", Arch. Hist. Exact Sci. , Vuelo. 15, 1975, pág.  67-114 .
50. Apéndice 3 de Szabó 2000 está dedicado enteramente a este concepto.
51. Bartel Leendert van der Waerden , “Defensa de una 'impactante' Punto de vista”, Arch. Hist. Exact Sci. , Vuelo. 15, núm. 3, 1976, pág.  199-210 .
52. Mahoney 1968 .
53. Burkert 1972 , p.  463.
54. Encontramos 11 ocurrencias en Caveing ​​1998a , p.  19.
55. DahanPeiffer , pág.  77.
56. Por ejemplo, ver (en) Jens Høyrup , Longitudes, anchuras, superficies: un retrato de la antigua álgebra babilónica y su parentesco [ detalles de la publicación ], p.  278 .
57. Adof P. Youschkevitch, "Matemáticas árabes (siglos VIII-XV)", Revue d'histoire des sciences , vol 30, 1977, p.  372 .
58. Caveing ​​1998a , p.  19.
59. Caveing ​​1998a , p.  33-75.
60. Christine Proust Matemáticas en Mesopotamia Site CultureMath (ENS Ulm - DESCO) (2006)
61. Benoît Rittaud ¡ A un matemático desconocido! Bibnum
62. No existe certeza sobre la naturaleza de la demostración de la época de Pitágoras, se plantean dos hipótesis y la que aquí se presenta es una de las dos. Sin embargo, ambas hipótesis asumen lados conmensurables: Éliane Cousquer ' El teorema de Pitágoras '
63. Caveing ​​1998b , p.  91.
64. La información de este párrafo sobre los pitagóricos está tomada de Burkert 1972 , p.  428.
65. Szabó 2000 , p.  153.
66. Esta idea la expresa Tannery, desarrollada extensamente por Szabó y explicada en J.-L. Périllié, El descubrimiento de lo inconmensurable y el vértigo del infinito , transcripción de una conferencia que tuvo lugar el 16 de mayo de 2001 en Grenoble, pág.  19-21 .
67. Una presentación está disponible en el sitio web: Éliane Cousquer ' El teorema de Pitágoras '
68. Jean Itard, Los libros de aritmética de Euclides, Hermann, 1961, p.  77 .
69. El análisis se propone en Jean-Louis Gardies , L'Héritage épistémologique d'Eudoxe de Cnidus: un ensayo de reconstrucción , Vrin ,2000, 156  p. ( ISBN  978-2-7116-0977-2 ) , pág.  67-79.
70. Se propone el análisis en Gardies 2000 , p.  79.
71. Zeuthen 1902 , p.  46.
72. Ver sobre este tema Radford 1991 .
73. Jean-Louis Gardies, Eudoxe y Dedekind , Revue d'histoire des sciences , vol. 37, n ° 37-2, 1984, pág.  111-125 .
74. DahanPeiffer , pág.  85-86.
75. Se expresan por primera vez por Jacques Peletier de Le Mans en 1554: IREM de Rennes François Viète Cap 11.8 p. 164
76. DahanPeiffer , pág.  110.

Artículo relacionado

Prueba sin palabras

Enlace externo

(en) Luigi Borzacchini, “  Álgebra geométrica  ” , en Dipartimento di Matematica, Università degli studi di Bari