Lógica difusa

La lógica difusa ( lógica difusa , en inglés) es una lógica de muchos valores en la que los valores de verdad de las variables, en lugar de ser verdaderos o falsos, son reales entre 0 y 1. En este sentido, amplía la lógica booleana tradicional con valores. De verdades parciales. Consiste en tener en cuenta varios factores numéricos para llegar a una decisión que se desea que sea aceptable.

Introducción

Por sus aspectos numéricos, la lógica difusa se opone a la lógica modal .

Formalizado por Lotfi Zadeh en 1965 , una herramienta de inteligencia artificial , se utiliza en campos tan variados como:

el automático (frenos ABS , control de proceso)
la robótica (reconocimiento),
gestión del tráfico rodado (semáforo en rojo),
el ATC ( gestión del tráfico aéreo )
el medio ambiente ( meteorología , climatología , sismología , análisis del ciclo de vida ),
el medicamento (ayuda al diagnóstico )
el seguro (selección y prevención de riesgos ) y muchos otros.

Está formalizado por una teoría matemática de conjuntos difusos de Lotfi Zadeh que presenta una extensión de la teoría de conjuntos clásicos a conjuntos definidos de manera imprecisa .

A partir de un concepto de función de pertenencia con valor en [0, 1], Lotfi Zadeh :

redefine lo que es un subconjunto de un universo dado,
construye un modelo completo de propiedades y definiciones formales,
muestra que esta teoría de subconjuntos difusos se reduce a la teoría de subconjuntos clásicos en el caso en que las funciones de pertenencia sólo toman valores binarios de {0,1}.

La lógica difusa tiene la ventaja de ser fácil de implementar, sin reclamar el rigor de una lógica probabilística (que también admite valores de verdad en el intervalo [0,1]), aunque esta última por sí sola es coherente en sentido estricto (ver Cox-Jaynes teorema ). Por ejemplo, la curva Ev (p) se puede reemplazar por tres segmentos de línea recta sin una pérdida excesiva de precisión para muchas aplicaciones consideradas anteriormente.

Principio

Al suavizar el álgebra booleana , la lógica difusa reemplaza el valor de verdad de una proposición que se elegirá en { verdadero , falso } por un grado de verdad, que se elegirá, por ejemplo, en [0, 1]. En lógica difusa, hay grados en la satisfacción de una condición.

Un ejemplo simple y antiguo es la docimología , es decir la evaluación de los alumnos de una clase: en cada disciplina esta se evalúa con una nota entre 0 (mala) y 20 (excepcional) y se estima el nivel del alumno para una orientación dada ponderando estas marcas con varios coeficientes dependiendo de la orientación considerada.

Propiedades

Tomemos el ejemplo de la velocidad de un vehículo en una carretera donde la velocidad normal es de 90 km / h . La velocidad se considera alta por encima de los 100 km / hy reglamentaria por debajo de los 80 km / h . Queremos caracterizar la velocidad del vehículo respondiendo, por ejemplo, a la pregunta "¿Es alta la velocidad?" ".

higo. 1

En este modelo de normativa vial, en lógica booleana, la respuesta a la pregunta se expresa de la siguiente manera (ver fig.1 ):

La velocidad aumenta un 100% por encima de los 100 km / hy un 0% por debajo.

En lógica difusa, diferentes grados de respuesta a la pregunta "¿Es alta la velocidad?" "(Ver fig. 2 ):

La velocidad es reglamentaria por debajo de 80 km / h . Por tanto, podemos decir que por debajo de 80 km / h , la velocidad es alta con una tasa de confianza del 0%.

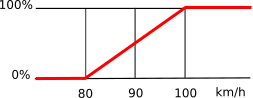higo. 2

La velocidad es alta por encima de los 100 km / h . La velocidad es ilegal con una tasa de confianza del 100% por encima de los 100 km / h .
En las etapas intermedias, la velocidad se considera ilegal con un 50% de confianza a 90 km / hy un 25% de confianza a 85 km / h .

Asimismo, podemos definir una función correspondiente a la pregunta "¿La velocidad es baja?" Como sigue (ver fig.3 ):

La velocidad es baja por debajo de 80 km / h . Por lo tanto, es bajo al 100%.

higo. 3

La velocidad no se considera en absoluto baja por encima de los 100 km / h . Por lo tanto, es bajo al 0%.
Por tanto, la velocidad es baja al 50% a 90 km / h , y al 25% a 95 km / h .

También podemos definir una función correspondiente a la pregunta "¿Es la velocidad media?" "(Ver fig. 4):

La velocidad es media a 90 km / h . A este ritmo, la velocidad es 100% media.

higo. 4

La velocidad no es en absoluto media por debajo de los 80 km / hy por encima de los 100 km / h . Fuera de este intervalo, la velocidad promedio es del 0%.
La velocidad es por lo tanto 50% de media en 85 kilometros / h y 95 kilometros / h .

La transición no tiene por qué ser lineal. Se pueden utilizar transiciones hiperbólicas (como una sigmoidea o hiperbólica ), exponencial , gaussiana (en el caso de un estado medio) o de cualquier otro tipo (ver fig. 5 ).

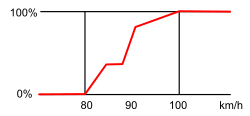higo. 5

Relaciones

El grado de verdad de una relación difusa entre dos o t objetos es el grado de pertenencia del par o del t-uple al conjunto difuso asociado con la relación.

Sea la relación 1 (es-a / es-a). Decir que cualquier silla es un mueble y que el 30% del mueble son sillas, otorgaremos un grado de verdad de 1 a est1 (silla, mueble) y un grado de 0,3 a est1 (pieza de muebles, silla) .

El conocimiento topográfico que posee un agente de un mundo cerrado puede basarse en la atribución de grados de verdad a una relación del estilo x est_near_of y than_de z , construida y / o refinada por el aprendizaje.

En general, las relaciones difusas permitirán codificar conocimientos graduados, empíricos o típicos, adquiridos directamente o por heurísticas, inducciones, etc.

Combinación de declaraciones

En el caso de una combinación de afirmaciones (por ejemplo: "Si el cielo es azul y si tengo tiempo "), surgen tres casos:

Los enunciados están vinculados por un "Y": en este caso, a esta conjunción se le puede asignar el grado más bajo de verdad. De hecho, basta con elegir un operador tal que where se llame norma t . es el más optimista de los estándares t. $\cima$ $\ top (x, y) \ leq \ min (x, y)$ $\cima$ $\ min$
Las entradas están unidas por una “O”: en este caso, a esta adición se le puede asignar el mayor grado de verdad. De hecho, basta con elegir un operador tal que where se llame t-conorm . es el más pesimista de los t-conorms. $\ Bot$ $\ bot (x, y) \ geq \ max (x, y)$ $\ Bot$ $\ max$
Se pueden negar una o más declaraciones. En este caso, para mantener un máximo de propiedades lógicas, asociamos la negación con el complemento del grado de verdad del enunciado.

Primer sistema

Definiendo los operadores lógicos básicos de la siguiente manera:

{\ Displaystyle Y: = mínimo; O: = máximo; NO (x): = 1-x}

es posible representar todas las operaciones lógicas básicas en lógica difusa:

Operador	Abreviatura	Solicitud
O	ORO	A O B [ ] $= máximo (A, B)$
Y		A y B $= min (A, B)$
NO		NO A $= 1-A$
O exclusivo	OUEX	A OUEX B $= máximo (A, B) -min (A, B)$
O	NO-O	A NI B $= 1-máx (A, B)$
NOSOTROS	NAND	A ON B $= 1 min (A, B)$
EQV	NO OUEX	A EQV B $= 1 + mínimo (A, B) -máx (A, B)$
RELOJ DE REPETICIÓN	REPS	REP A $= A$

Propiedades y limitaciones Este sistema conserva muchas propiedades booleanas, pero no la no contradicción : si tiene por grado de verdad , tiene por grado de verdad y su conjunción , con valor en ...

A

v

NO (A)

1-v

min (v, 1-v)

[0,0.5]

Segundo sistema

Además, la dimensión numérica de las variables de lógica difusa permite utilizar otras operaciones:

El producto: A × B para AND (que pierde la idempotencia : A AND A se convierte entonces en una interpretación de la misma A );
La composición: A + B - A × B para OR (la simple adición excedería los límites del intervalo [0 1] en ciertos casos).
Manteniendo NON (v) = 1-v, todavía mantenemos muchas propiedades lógicas.

Otros sistemas

Para combatir ciertos problemas de inferencia, es posible que deseemos un operador AND más difícil, asociando la operación A AND B con el grado . $máx. (A + B-1.0)$

En tal caso, O y NO deben elegirse para preservar o no ciertas propiedades, por ejemplo para asegurar el razonamiento. Se encontrarán en la Teoría de Posibilidades (op. Cit.) Las relaciones entre los axiomas lógicos deseados y las ecuaciones funcionales que los operadores correspondientes deben respetar.

Incluso podemos cambiar el espacio de verdad, prefiriendo, por ejemplo, [-1 +1] para ciertas propiedades bipolares.

Operadores difusos

Los operadores difusos se pueden definir de varias formas, ya que dotan, según Goguen, al espacio de verdad elegido con una estructura de celosía, deseable para AND y OR , una celosía preferiblemente complementada para un NOT involutivo.

Las familias paramétricas de operadores difusos permitirán que el mismo motor de inferencia incorpore lógicas más o menos estrictas. Por tanto, la misma aplicación podrá recurrir a diferentes implementaciones elegidas juiciosamente de acuerdo con el contexto.

El siguiente ejemplo muestra a través de 3 modos de resolución la influencia de la elección de los operadores, más allá de un enfoque ingenuo de un problema.

Ejemplo de uso

Este ejemplo muestra cómo combinar operadores difusos de varios tipos a través del problema "confirmar la pertenencia de una persona a un grupo":

Estados Una persona será más o menos miembro (a nivel de fzMember , entre 0 y 1, inclusive) de un grupo, digamos amantes de las flores , o si, por alguna razón, ya son más o menos parte de él (a fzDejaMembre nivel ), ya sea si tiene un conocimiento bastante bueno de las orquídeas ( fzConnaitOrchidees ) y ese conocimiento de las orquídeas es un criterio bastante decisivo ( fzOrchideesAmis ) para pertenecer al grupo de los amantes de las flores . Solucion 1 fzMembre = Zadeh_OR(fzDejaMembre, Multiply_AND(fzConnaitOrchidees, fzOrchideesAmis))

Zadeh OR
Multiplica Y
(paraboloide hiperbólico)

ImplementaciónfzMembre = max(fzDejaMembre, (fzConnaitOrchidees * fzOrchideesAmis)) pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve 0.7 pour fzDejaMembre=0.7, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.72 pour fzDejaMembre=0.72, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on retrouve 0.72 pour fzDejaMembre=0.72, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on conserve 0.72 (ce qui est le résultat vraisemblablement attendu) Solución 2: use solo operadores Zadeh

Una solución que solo usaría operadores Zadeh sería:

fzMembre = Zadeh_OR(fzDejaMembre, Zadeh_AND(fzConnaitOrchidees, fzOrchideesAmis))

Zadeh OR
Zadeh Y

ImplementaciónfzMembre = max(fzDejaMembre, min(fzConnaitOrchidees, fzOrchideesAmis)) pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=1 (vrai), on trouve 0.778 pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve aussi 0.778 (ce qui est trop élevé) pour fzDejaMembre=0.778, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.8 pour fzDejaMembre=0.8, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on retrouve 0.8 pour fzDejaMembre=0.8, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on conserve 0.8 (ce qui est stable mais trop élevé) Solución 3 - Operadores representables por paraboloides hiperbólicos

Una solución que solo usaría operadores representables por paraboloides hiperbólicos sería:

fzMembre = Add_OR(fzDejaMembre, Multiply_AND(fzConnaitOrchidees, fzOrchideesAmis))

Agregar OR
(paraboloide hiperbólico)
Multiplica Y
(paraboloide hiperbólico)

ImplementaciónfzMembre = fzDejaMembre + (fzConnaitOrchidees*fzOrchideesAmis) - (fzDejaMembre*fzConnaitOrchidees*fzOrchideesAmis) pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve 0.7 pour fzDejaMembre=0.7, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.916 (ce qui est sûrement trop élevé) pour fzDejaMembre=0.916, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0,97648 (ce qui est instable et sûrement beaucoup trop élevé) pour fzDejaMembre=0,97648, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on trouve 0. 987 064 (une augmentation bien malvenue) Convergencia - Revisión de las soluciones presentadas

Los tres métodos discutidos anteriormente convergen cuando los valores de entrada son booleanos:

pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0 (faux) et fzOrchideesAmis=1 (vrai), on trouve 0 (faux) pour fzDejaMembre=0 (faux), fzConnaitOrchidees=1 (vrai) et fzOrchideesAmis=1 (vrai), on trouve 1 (vrai) pour fzDejaMembre=1 (vrai), fzConnaitOrchidees=1 (vrai) et fzOrchideesAmis=1 (vrai), on retrouve 1 (vrai) pour fzDejaMembre=1 (vrai), fzConnaitOrchidees=0 (faux) et fzOrchideesAmis=1 (vrai), on conserve 1 (vrai)

El operador implica

Definición

Para el ejemplo de orquídeas anterior, una situación normal es que conocer las orquídeas implica pertenecer a un grupo. Es decir, más precisamente, que no se pueden conocer las orquídeas y , al mismo tiempo, no formar parte del grupo de amigos de las flores .

fzImpliqueOk = NOT(AND(fzConnaitOrchidees, NOT(fzMembre)))

Tal como vimos anteriormente, varias formas de implementar los operadores OR y AND, también hay varias formas de implementar la noción de implicación.

fzImpliqueOk = Bool_IMPLIES(fzConnaitOrchidees, fzMembre) fzImpliqueOk = Zadeh_IMPLIES(fzConnaitOrchidees, fzMembre) fzImpliqueOk = HypPar_IMPLIES(fzConnaitOrchidees, fzMembre)

Implica booleano
Zadeh IMPLÍCITO
Paraboloide hiperbólico
IMPLICA

Implementación

Los operadores anteriores se implementarán respectivamente así:

fzImpliqueOk = fzConnaitOrchidees ⇐ fzMembre fzImpliqueOk = 1 - min(fzConnaitOrchidees, (1 - fzMembre)) fzImpliqueOk = 1 - fzConnaitOrchidees + (fzConnaitOrchidees*fzMembre)

en un caso extremo pero normal , con fzKnownOrchids = 0.8 y fzMember = 0.995, los valores encontrados serán respectivamente:

1 (true) 0.995 (Zadeh) 0.996 (Hyperbolic Paraboloid)

en un caso considerado como normal , con fzKnownOrchids = 0.8 y fzMember = 0.72, los valores encontrados serán respectivamente:

0 (false) (la personne est moins membre qu'elle ne connait) 0.72 (Zadeh) 0.776 (Hyperbolic Paraboloid)

en otro caso que sigue siendo normal , la persona también puede ser miembro de los amigos de las flores por su amor a los tulipanes, con fzKnownOrchids = 0.66 y fzMember = 0.72, los valores encontrados serán respectivamente:

1 (true)(la personne est plus membre qu'elle ne connait) 0.72 (Zadeh) 0.772 (Hyperbolic Paraboloid)

en un caso bastante dudoso , con fzKnownOrchids = 0.5 y fzMember = 0.5, los valores encontrados serán respectivamente:

1 (true) 0.5 (Zadeh) 0.75 (Hyperbolic Paraboloid)

en un caso anormal , con fzKnownOrchids = 0.8 y fzMember = 0.3, los valores encontrados serán respectivamente:

0 (false) 0.3 (Zadeh) 0.44 (Hyperbolic Paraboloid)

en un caso anormal y extremo, con fzKnownOrchids = 0.8 y fzMember = 0.005, los valores encontrados serán respectivamente:

0 (false) 0.2 (Zadeh) 0.204 (Hyperbolic Paraboloid) Uso práctico

Una aplicación informática que pretenda ofrecer a un operador humano el tratamiento de casos anormales empezando por los más sospechosos utilizaría los valores indicados anteriormente en negrita y obtenidos por el método identificado como Paraboloide Hiperbólico , que es particularmente discriminatorio.

No es seguro que esta aplicación sea de interés para los amigos de las flores . Por otro lado, el interés por un servicio de medicina preventiva (o incluso por una floristería) es comprensible. Cuando se debe limitar el número de exámenes de casos sospechosos (por ejemplo, por razones de tiempo, costo, peligrosidad, etc.), una clasificación previa inteligente basada, si no en una teoría indiscutible, al menos en una tecnología operativa, puede resultar útil. .

Representación gráfica

Los artículos comunes del artículo : el operador difuso proporciona muchas representaciones gráficas de algunas posibles implementaciones de los operadores difusos. On trouvera ci-dessous, à titre d'exemple, la représentation de huit implémentations différentes d'une opération qui viserait à apprécier la simultanéité de deux faits (jugés de poids équivalents dans les six images à gauche mais de poids différents dans les deux images De derecha).

zadeh-Y
multiplicar-Y
yager-AND
mm-PESO-O-Y

zadeh-OR
añadir OR
yager-OR
mm-PESO-Y-O

Operadores lingüísticos

Sea v (x es caliente) = 0.8. Podemos establecer v (x es muy caliente) = 0,8² = 0,64 e inversamente v (x es bastante caliente) = rac2 (0,8) = 0,89, lo que facilita la codificación del conocimiento empírico.

Comando difuso

Una vez evaluado el valor de la entrada (“¿Es la velocidad alta?”), Se puede determinar un valor para una función de salida. Considere la regla "Si la fiebre es alta, administre aspirina". Esta regla se llama control difuso . Consta de dos partes:

Una entrada: "¿Tiene fiebre alta? ". Consideramos que la fiebre no es fuerte por debajo de 38 ° C , y está muy por encima de 40 ° C .
Una salida: "Administrar aspirina"

Estas dos partes están vinculadas. Se pueden representar juntos como en la fig. 6.

higo. 6

Existen varias técnicas para determinar el valor de la salida (en el ejemplo: la cantidad de aspirina a administrar):

La línea que tiene la misma ordenada que el punto de la curva inicial que tiene el valor de entrada como abscisa interseca la curva de salida. La abscisa de este punto de intersección es un posible valor de salida (fig. 7).

higo. 7

La recta que tiene la misma ordenada que el punto de la curva inicial que tiene por abscisas el valor de la entrada delimita un trapezoide al nivel de la salida. El centro de gravedad de este trapezoide también es un posible valor de salida (fig. 8).

higo. 8

Límites y críticas a la teoría

¿Deficiencias como teoría?

Existe una opinión que dice que “La teoría de conjuntos difusos presenta la peculiaridad de no tener teorema que proponer. Es decir que si puede prestar algunos servicios técnicos, no puede por todo ello reclamar ningún estatus de ciencia, y menos de teoría ”.

De hecho, se ha formalizado la lógica difusa y un teorema (elemental, sin embargo) muestra que en el caso particular donde las proposiciones procesadas no son borrosas, la lógica borrosa se reduce a lógica clásica.

En su obra Rational Decisions in Uncertain , Myron Tribus recuerda que el teorema de Cox-Jaynes muestra, por un lado, que se puede representar un estado de conocimiento incierto mediante una probabilidad y, por otro, que cualquier medio utilizado para tomar decisiones será isomorfo a la teoría de la probabilidad o inconsistente. El conocimiento difuso no es un conocimiento incierto estrictamente hablando : podemos, por ejemplo, saber con precisión que un hombre mide 1,74 m de altura . Sin embargo, lo que no está claro es si se considerará "grande" o "pequeño".

Por el contrario , decir: "la edad de esta persona se acerca a los 30 años" representa una estimación vaga de la edad efectiva de la persona, que por su parte es muy precisa. La imprecisión se refiere a la estimación en sí y no a la edad real.

También podríamos decir: "la edad de esta persona está entre 27 y 33 años, con una probabilidad de 0,8". Aquí nuevamente, la probabilidad mide un estado de conocimiento del observador y no una característica de lo que se observa.

Jim Bezdek distingue por su parte probabilidad e imprecisión: “Estamos en un desierto, después de días de vagabundeo… Casi muerto de sed, encontramos dos botellas llenas de un líquido. En la botella A, una etiqueta dice " bebible con un grado de 0,9", y en la botella B, la etiqueta dice "bebible con una probabilidad de 0,9". ¿Cuál de estas dos botellas deberíamos elegir? ". Si traducimos las indicaciones de las etiquetas, eliminamos que bebiendo la botella A, podemos salirnos con los únicos riesgos, algunos problemas intestinales no fatales ... En cambio, bebiendo la botella B, hay una no probabilidad insignificante (10% de probabilidad) de que el líquido pueda ser muy dañino (ácido ...) y absolutamente no potable.

Se introdujo una teoría de las posibilidades (también por Lotfi Zadeh en 1978) para permitir la consideración combinada de la imprecisión y la incertidumbre en el conocimiento.

La lógica difusa no es la única que habla de incertidumbre

La lógica modal fue introducida por Aristóteles , y luego continuada por Leibniz y los investigadores contemporáneos para reflejar las deficiencias o mejoras de las afirmaciones presentes en los lenguajes naturales, centrándose, por ejemplo, en los informes de verdadero, falso, necesario y posible.

La teoría de la complejidad algorítmica (o complejidad de Kolmogorov ) es también un método más o menos riguroso para considerar la dificultad de dar la descripción precisa de una cosa (X puede parecer más complejo que Y para una máquina A y menos complejo que Y para una máquina B, por ejemplo, una computadora cuántica, es por lo tanto una complejidad relativa a una máquina de referencia dada .

Finalmente, las probabilidades bayesianas utilizadas en un futuro incierto utilizan enfoques similares a los de la lógica difusa, pero esta vez sin arbitrariedad: las distribuciones de probabilidad a priori deben ser las de máxima entropía ...

Notas y referencias

Novák, V. , Perfilieva, I. y Močkoř, J. , Principios matemáticos de la lógica difusa , Dordrecht, Kluwer Academic,1999, 320 p. ( ISBN 978-0-7923-8595-0 , leer en línea )
Sistema de Zadeh que puede considerarse inspirado por Lukasiewicz
escritura ligera: estrictamente hablando, debemos distinguir el enunciado A y su grado de verdad v (A), y escribir v (A OR B) = max (v (A), v (B))
en un estilo cercano a George Boole (1854), o Vallée quien llama a esta composición produel en su Binary Analysis ; a veces también visto como probabilístico

Ver también

Godjevac J., Ideas sobre lógica difusa , PPUR: Lausanne, collection informatique, 1999, 128p., ( ISBN 2-88074-378-8 ) . Prade H., Dubois D. & al., Teoría de las posibilidades: aplicaciones a la representación del conocimiento en la informática , coll. (Método + programas), Masson: París, 1985.